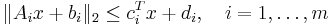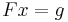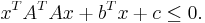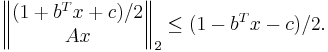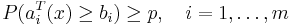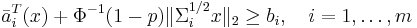Second-order cone programming

A second-order cone program (SOCP) is a convex optimization problem of the form

minimize 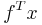$\ f^T x \$ subject to

$\lVert A_i x %2B b_i \rVert_2 \leq c_i^T x %2B d_i,\quad i = 1,\dots,m$

$Fx = g \$

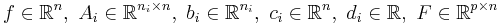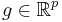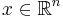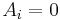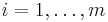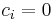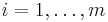where the problem parameters are $f \in \mathbb{R}^n, \ A_i \in \mathbb{R}^{{n_i}\times n}, \ b_i \in \mathbb{R}^{n_i}, \ c_i \in \mathbb{R}^n, \ d_i \in \mathbb{R}, \ F \in \mathbb{R}^{p\times n}$ , and $g \in \mathbb{R}^p$ . Here $x\in\mathbb{R}^n$ is the optimization variable. When $A_i = 0$ for $i = 1,\dots,m$ , the SOCP reduces to a linear program. When $c_i = 0$ for $i = 1,\dots,m$ , the SOCP is equivalent to a convex Quadratically constrained quadratic program. Semidefinite programs subsumes SOCPs as the SOCP constraints can be written as Linear Matrix Inequalities(LMI) and can be reformulated as an instance of semi definite program. SOCPs can be solved with great efficiency by interior point methods.

1 Example: Quadratic Constraint
2 Example: Stochastic Programming
3 Solvers
4 References
5 External links

Example: Quadratic Constraint

Consider a quadratic constraint of the form

$x^T A^T A x %2B b^T x %2B c \leq 0.$

This is equivalent to the SOC constraint

$\left\| \begin{matrix} (1 %2B b^T x %2Bc)/2\\ Ax \end{matrix} \right\|_2 \leq (1 - b^T x -c)/2.$

Example: Stochastic Programming

Consider a stochastic linear program in inequality form

minimize 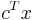$\ c^T x \$ subject to

$P(a_i^T(x) \geq b_i) \geq p, \quad i = 1,\dots,m$

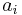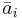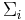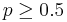where the parameters $a_i \$ are independent Gaussian random vectors with mean $\bar{a}_i$ and covariance $\Sigma_i \$ and $p\geq0.5$ . This problem can be expressed as the SOCP

minimize 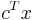$\ c^T x \$ subject to

$\bar{a}_i^T (x) %2B \Phi^{-1}(1-p) \lVert \Sigma_i^{1/2} x \rVert_2 \geq b_i , \quad i = 1,\dots,m$

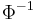where $\Phi^{-1} \$ is the inverse error function.

Solvers

There are various solvers available for solving SOCP. Some of the popular ones are listed below

1. Free and opensource, with OSI-Approved licenses

Name	License	Brief info
CSDP	CPL	a library of routines that implements a predictor corrector variant of the semidefinite programming algorithm of Helmberg, Rendl, Vanderbei, and Wolkowicz
DSDP	GPL	is present in Linux software channels
OpenOpt	BSD	universal cross-platform numerical optimization framework; see its SOCP page and full list of problems
SBmethod	GPL	no longer supported
SDPT3	GPL2	API: MATLAB (commercial); last update - December 2002
SDPA	GPL	primal-dual interior-point method
SDPLR	GPL?	language: C, API: MATLAB
SeDuMi	GPL?	package for commercial MATLAB
CVXOPT	GPL	a comprehensive Python library for convex optimization

2. Commercial

MOSEK — The first commercially available software package for solution SOCP. with Free Academic Licence.
CPLEX — Full-featured solver for large scale linear, quadratic, and integer programming problems, including SOCP
PENSDP
LOQO

Note that the most of the solvers in the above list are more general solvers (i.e they solve Semidefinite Programs or more general Convex optimization problems). There have been a few benchmarking studies comparing the various solvers ^[1]^[2]

References

^ H.D Mittelmann (2003). "An independent benchmarking of SDP and SOCP solvers". Mathematical programming (Springer) 95 (2): 407–430. doi:10.1007/s10107-002-0355-5.
^ SDP Benchmark results

External links

Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 15, 2011.